时讯动态
媒体关注
政策支持
研究院获批承担ISO/IEC JTC 3国内技术对...
2024-04-28
陈玖朋荣获PhotoniX Prize技术突破奖
2024-04-18
【转载】潘建伟:百年量子,量子信息方兴未艾
2024-04-15
合肥国家实验室管理人员招聘启事
2024-04-10
量子技术赋能政府管理 器件无关量子随机数助力食品安...
2024-04-01
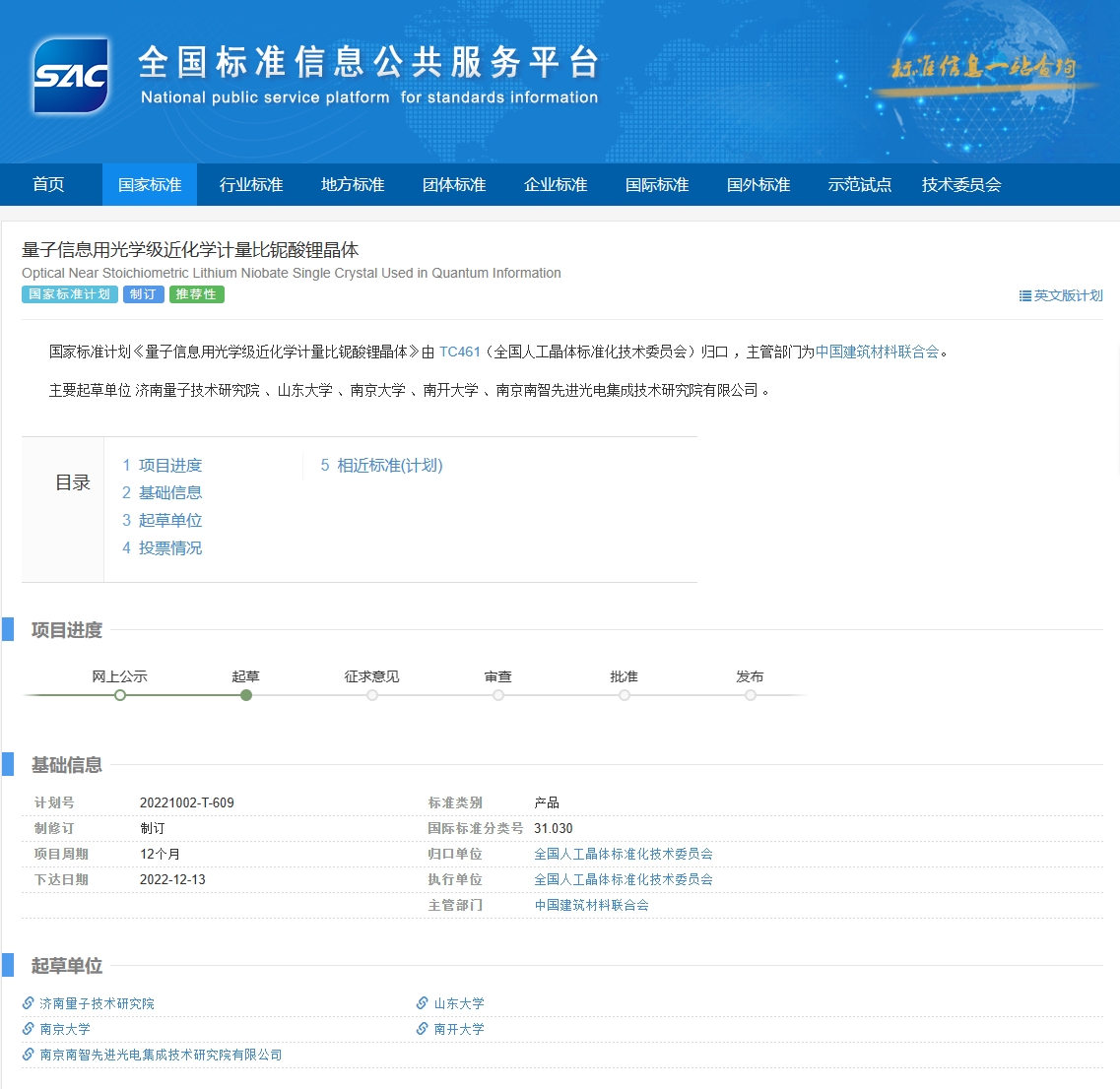
我国首批量子测量领域国家标准正式发布
2024-03-21
【转载】陆朝阳教授谈量子计算的产业泡沫:在乐观和不...
2024-03-21
更多
公示公告
-
2023-09-04
-
2022-10-28
-
2021-04-07
-
2021-03-31
-
2021-03-17
人才引进
党群工作